Uff, narobiłem się. Ale po kolei. Wszystko zaczęło się dość dawno już, od wpisu z fortepianami Fermiego, tygrysami i CIA. W zeszłym roku kontynuowałem moją rozprawę z kiepskim zarządzaniem ryzykiem cyberbezpieczeństwa mikro-serią: A do czego jest ta rura? cz.1 i druga. Na deser był Bayes.
Jestem zadowolony z treści i formy tamtych wpisów, ale to jeszcze nie było to. To “to” właśnie się zmaterializowało. A wszystko zaczęło się od intensywnego kursu przypominania sobie i rozwijania Pythona świetnie opracowanego i prowadzonego przez wykładowców uniwersytetu stanowego w Michigan. Python jest mi potrzebny do paru innych rzeczy, więc połowę tego kursu połknąłem w tydzień. Zacząłem sobie wymyślać jakieś przydatne i praktyczne juzkejsy. I nagle.. “hello! ..I am here!” Zawołała do mnie z półki moja ulubiona zielona książka, machając przy tym swoimi małymi zielonymi łapkami. “I am your goddamn usecase!” wrzasnęła..
Czym innym jest opowiadać na lewo i prawo jak świetną książkę napisali panowie Hubbard i Seiersen, a czym innym zupełnie zademonstrować jak działa ilościowa metoda szacowania ryzyka w cyberbezpieczeństwie (ale nie tylko). Przed kontynuacją czytania tego wpisu, polecam przypomnieć sobie poprzednie wpisy, od tygrysów, przez rury po Bayesa. Sam tak właśnie zrobiłem. Ważny jest kontekst. Przedstawiona tutaj ilościowa metoda analizy ryzyka opiera się na rachunku prawdopodobieństwa, zwykłej prostej algebrze z odrobiną statystyki. Od tego jest właśnie rachunek prawdopodobieństwa i statystyka aby nasze estymacje dotyczące oceny szans czy możliwości materializacji ryzyka (czyli oddziaływania jakichś zidentyfikowanych i opisanych zagrożeń) w naszych niedoskonałych i podatnych na owe zagrożenia (nie na ryzyka!!!) systemach IT.
Właściwa estymacja powinna opierać się na danych, tych które mamy w firmie, bądź takich do których możemy dotrzeć w internecie (chociażby coroczny raport Verizona). Nasze zdarzenia zagrożeń, mogą być też bezpośrednim wynikiem zastosowania metodyki MITRE ATT&CK lub chociażby STRIDE (dla jakiegoś projektu rozwiązania). Do tego odpowiednio dobrane grono ekspertów powinno samodzielnie i osobno popracować nad estymacją listy takich zdarzeń. Dlaczego osobno? Otóż dlatego, że jako stworki stadne, leniwe i sprytne, mamy wpływ na innych w takim sam sposób jak inni mają wpływ na nas. Na przykład dla świętego spokoju czy też z niemania-i-niechcenia-mania-pojęcia po prostu zgodzimy się z innymi na takiej nasiadówie, byleby tylko ją szybko skończyć w poczucie dobrze odwalonej pracy. Ale ok, żarty na bok. Chodzi o to by łatwiej zidentyfikować i uzasadnić ewentualne rozbieżności przy wynikach estymacji dla konkretnych osób. Pamietamy, że nasze mózgi mają swoje ograniczenia gatunkowe. Szybkie myślenie, problemy z prawdopodobieństwem jako takim, intuicja, zakotwiczenie, zbytnia pewność siebie, itd. Czy już mówiłem? polecam tę zieloną książkę.. i parę innych (wymienionych we wpisach na tym blogu.
Mamy więc listę dziesięciu zdarzeń, których P wyestymowaliśmy, biorąc pod uwagę rozmaite dane własne, raporty i statystyki dostępne z internetu, następnie wykonany rachunek Bayesa, wyniki porównane z innymi. Dotyczy to również przedziału strat. Konkretnie parametryzujemy sobie takie zdarzenie, przydzielając mu określone P w ciągu roku (12 miesięcy), oraz przedział możliwych strat z 90% poziomem ufności.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
events = {
"event1": (0.21, 100000, 550000, "Successful DDoS on the cloud base core app"),
"event2": (0.08, 500000, 1500000, "Sensitive data exfiltration"),
"event3": (0.15, 200000, 1000000, "Malicious code injected into production pipeline"),
"event4": (0.38, 10000, 100000, "Laptop with sensitive data lost/stolen"),
"event5": (0.17, 15000, 50000, "Malicious code in 3rd party dependencies"),
"event6": (0.15, 1000, 150000, "Broken backups"),
"event7": (0.04, 1000000, 12000000, "Malware attack, knocked out internal network"),
"event8": (0.05, 10000, 500000, "Insider's threat"),
"event9": (0.03, 1000000, 11500000, "Terrorist attack"),
"event10": (0.25, 5000, 50000, "Broken app release")
}
Mamy również oszacowany mityczny “apetyt na ryzyko” czy też “tolerancję na ryzyko” po dłuższej dyskusji z naszymi “finansowymi”. Rozkład ewentualnych strat z oszacowanym prawdopodobieństwem wystąpienia w przeciągu 12 miesięcy. Wiadomo, małe straty to wyższa akceptacja dla ich wystąpienia, wysokie straty to niższa i bardzo niska. Czyli nieakceptowalna. Ten krok jest nie mniej ważny od poprzedniego.
1
2
3
4
5
6
7
8
9
10
risk_tolerance = [
(100000, 90),
(250000, 50),
(500000, 30),
(750000, 15),
(1000000, 2),
(10000000, 0.2)
]
Do kompletu naszych danych wejściowych potrzebujemy jeszcze listę ewentualnych wdrożeń z dziedziny bezpieczeństwa i cyberbezpieczeństwa. Mogą to być działania planowane, nie-planowane. Idzie o to aby pokazać jak nakłady na tę dziedzinę ponoszone przez firmę wpływają na szanse wystąpienia różnych ryzyk. Albowiem właśnie po to są wdrożenia w cyberbezpieczeństwie. Warto więc sprawdzić czy coś dają. Tutaj pod ten konkretny przykład utworzyłem listę 1-do-1 ze zdarzeniami zagrożeń. Możemy to jednak przedstawiać w różnej formie, a potem w kodzie odpowiednio warunkując. Np. Wdrożenia ABC dotyczy zdarzeń: 1,3,4,7 dla każdego estymujemy że wpływ na wystąpienie spadnie o dany % (to ta druga liczba w krotce poniżej, pierwszą jest symulowana wartość inwestycji w cyberbezpieczeństwo).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
sec_controls = {
"event1": (70000, 0.65),
"event2": (200000, 0.55),
"event3": (77000, 0.7),
"event4": (30000, 0.37),
"event5": (25000, 0.42),
"event6": (100000, 0.62),
"event7": (230000, 0.85),
"event8": (121000, 0.47),
"event9": (130000, 0.6),
"event10": (25000, 0.45)
}
Nasz wehikuł metodyczny nabiera prędkości. Przed Państwem - Monte Carlo! Metoda Monte Carlo jest szeroko stosowana w zarządzaniu ryzykiem w wielu obszarach - finansowym, wydobywczym, wszędzie tam gdzie zamiast “best educated guess” panuje logika, matematyka i dbałość o własne pieniądze. Skąd się wzięła? Wymyślił ją wielki polski matematyk Stanisław Ulam. Był chory i stawiał z nudów jakiegoś trudnego pasjansa. Wtedy zdał sobie sprawę, że bardzo trudno byłoby obliczyć, jakie było prawdopodobieństwo powodzenia tego pasjansa. Natomiast w miarę łatwo, jak sądził, można by było zamodelować to z pomocą komputera. Taki komputer który mógłby przeprowadzić bardzo wiele prób, dzięki czemu można by zaobserwować rozkład prawdopodobieństwa powodzenia pasjansa. Ponoć nazwa wzięła się ze skojarzenia z wujem profesora Ulama, który zwykł pożyczać pieniądze od rodziny, po czym radośnie przepuszczać je właśnie w Monte Carlo.
Metoda ta posłuży tutaj do zamodelowania rozkładu prawdopodobieństwa wystąpienia zdarzenia i związanej z nim straty. Posługując się generatorem losowym Pythona i metodą Monte Carlo sprawdzimy 10 tysięcy razy dla tych 10 zdarzeń (każdy), czy zdarzenie wystąpi, a jeśli tak to z jaką losowo wygenerowaną stratą z przedziału. Jeśli zdarzenie nie wystąpi, strata wynosi 0. Mamy już jeden rozkład, który stanowi dla nas niejako benchmark dla porównania z naszymi wynikami - nasza “tolerancja na ryzyko”. Zakres strat przypisany do każdego zdarzenia nie będzie zamodelowany rozkładem normalnym - czyli takim, gdzie najprawdopodobniej strata losowa wypadnie nam gdzieś po środku przedziału. Będzie zamodelowana rozkładem logarytmicznie normalnym (log-normalnym). A to taki rozkład, gdzie najbardziej prawdopodobne liczby z naszego przedziału wyskakują bardziej przy jego początku i są mniej prawdopodobne przy końcu takiego przedziału. Dlaczego tak? Weźmy pod uwagę naturę incydentów czy zdarzeń w obszarze cyberbezpieczeństwa. Jest to statystycznie pewne - że występuje daleko więcej zdarzeń o małej bądź nawet znikomej wartości strat, od zdarzeń których konsekwencje są znaczne albo nawet katastrofalne. Stąd asymetria kształtu względem rozkładu normalnego. Ponad to, wartości występujące w tym rozkładzie mogą być tylko równe lub większe od zera.
Jeśli zdarzenie zaistniało w naszej symulacji to wyliczamy medianę i odchylenie standardowe i zwracamy wartość straty wygenerowanej losowo dla tak sparametryzowanego rozkładu.
1
2
3
4
5
6
7
8
def threat_event_loss(lower_bnd, upper_bnd):
"""If threat event occured, let's get its loss it inflicts,
given lower and upper bounds of 90% CI"""
mean = (np.log(lower_bnd) + np.log(upper_bnd))/2
std_deviation = (np.log(upper_bnd) - np.log(lower_bnd))/3.29
return round(float(np.random.lognormal(mean, std_deviation)),2)
I tak postępujemy 10 tysięcy razy dla całej listy naszych zdarzeń. Zwrotnie dostaniemy dystrybucję takich strat na wykresie:
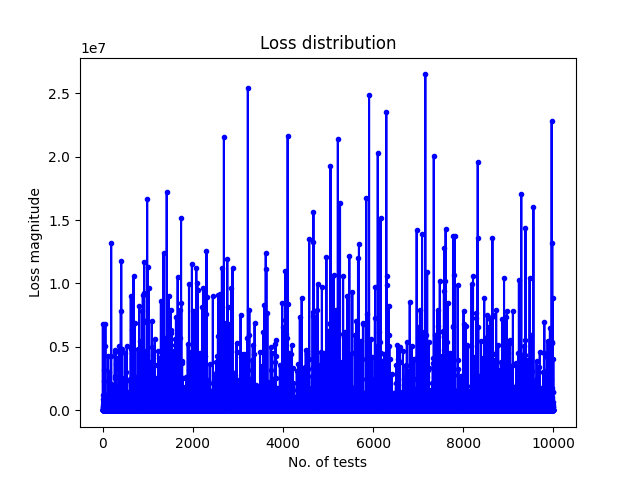
Tak samo postępujemy z wariantem, w którym scenariusze naszych przypadków kompensowane są naszymi inwestycjami w cyberbezpieczeństwo z oszacowanym wpływem na wystąpienie zdarzenia.
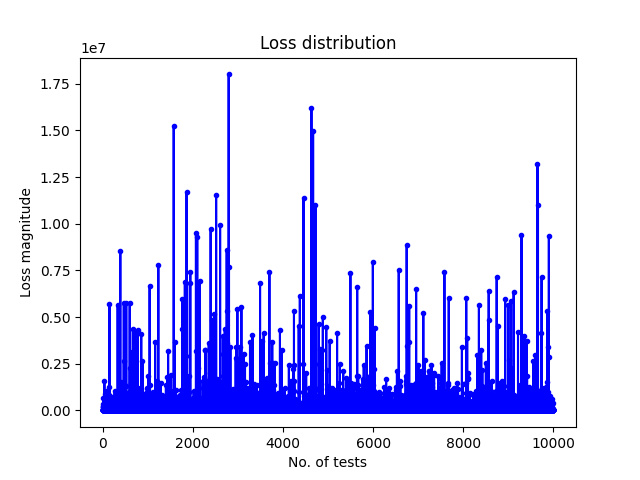Już na pierwszy rzut oka widać, że dystrybucja i gęstość zdarzeń ze stratami jest mniejsza niż bez środków kompensujących.
Jedna rzecz, którą warto mieć na uwadze wprowadzając estymaty zakresu strat dla zdarzeń. Jeśli przyjmiemy zakres gdzie jego dolna wartość będzie o rzędy wielkości mniejsza od górnej wartości to możemy dostać dość nierealne wygenerowane wartości. Trzymajmy się zasady że maksymalna różnica to jeden rząd wielkości. Np. 10 tys. do 100 tys.
Funkcje loss_distribution i loss_distribution_reduced zapewniły nam dystrybucje strat i wygenerowały dane wejściowe (w postaci listy list kolejnych prób) do wygenerowania krzywej strat w funkcji prawdopodobieństwa.
To ten kawałek kodu w sekcji #run:
1
2
3
4
losses_no_ctrls = loss_distribution(events, NO_SIMULATIONS)
losses_with_ctrls = loss_distribution_reduced(events, sec_controls, NO_SIMULATIONS)
Te zmienne stają się argumentem dla wywołania funkcji generującej odpowiednio: wykres dla strat bez kompensacji i z kompensacją:
1
2
3
4
plot_loss_exceedance(loss_exceedance_curve(losses_no_ctrls, STEP), risk_tolerance, "Fig-3.png")
plot_loss_exceedance(loss_exceedance_curve(losses_with_ctrls, STEP), risk_tolerance, "Fig-4.png")
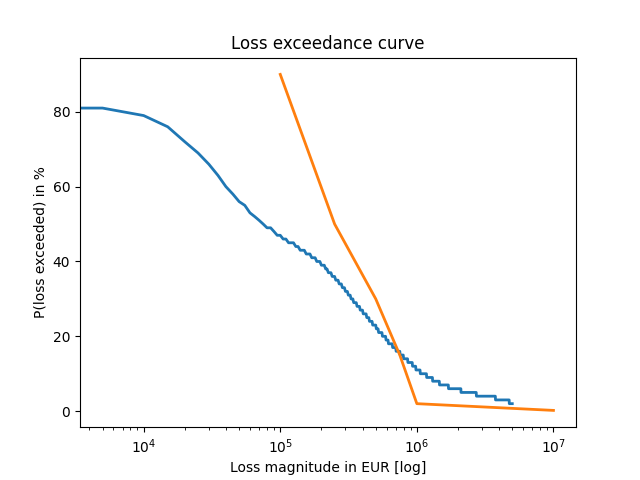
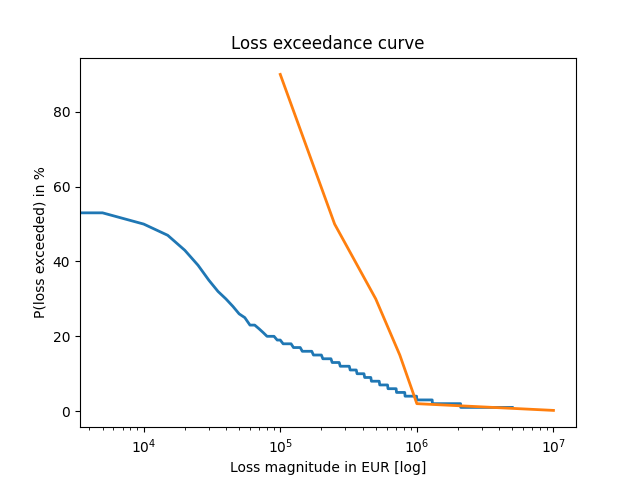
Dodatkowo w wyniku otrzymujemy wartości średniej oczekiwanej straty dla obu wariantów i nakłady finansowe na program komensacji tych ryzyk:
(python-exercises) 18:51:25:[python-exercises/distros] >> python3 cyberrisk_sim_multi.py
Average loss: 558,023.05 EUR with no controls in place
Average loss: 175,437.74 EUR with controls in place
Total security investments: 1,008,000.00 EUR
Na podstawie takich wyników można wysnuć całkiem konkretne wnioski. Na przykład:
- W wyniku nakładów w wysokości ~1mln EUR średnia oczekiwana strata spada nam mniej więcej 2.5 krotnie w ciągu roku. Przy czym prawdopodobieństwo jej wystąpienia spada dwukrotnie (z ok. 40% do ok. 20% - patrząc na wykresy 3 i 4)
- W wyniku tychże nakładów nasze ryzyka mieszczą się w założonej tolerancji na ryzyko, gdzie bez tych nakładów, straty powyżej 1 mln EUR są powyżej założonej tolerancji (wykres 3).
- Widać, że po wdrożonym programie kompensacji ryzyk, nawet te straty o niskiej wartości są mniej prawdopodobne o ok. połowę.
- Widać wyraźnie, że powinniśmy się skupić na zagrożeniach i podatnościach w naszym IT, które moga przynieść bardzo wysokie straty, pomimo niskiej szansy ich wystąpienia.
- Widać wreszcie, jak można zamodelować koszty w bezpieczeństwie i bez ich wydawania, po prostu wspomóc efektywniejsze planowanie.
Podsumowując, analiza ilościowa bazująca na faktach, przy możliwie poprawnej estymacji, biorąc pod uwagę fakty i przetwarzając to logicznie i matematycznie, da nam wiele równie konkretnych i pomocnych odpowiedzi, których nie da nam żadna najbardziej kolorowa heatmapa. Kluczową sprawą jest tutaj jakość estymacji.
Kod nie jest ani finezyjny ani optymalny, ale działa. Będę jeszcze nad nim pracował, rozwijał. Pewnie jak się douczę modułu pandas będę mógł z tym zrobić o wiele więcej i pewnie szybciej. Przedstawioną metodę, można też rozwinąć dodając rachunek Bayesa i zdarzenia zależne - jeśli event1 zaistniał to event3 jest bardziej prawdopodobny, bo otwiera możliwość ataku z wielu kierunków. Ogólnie rzecz biorąc, temat nie jest łatwy i trzeba mu poświecić sporo uwagi i czasu. Aczkolwiek jeśli pracownikom pytającym o bonus roczny, nie odpowiadamy, że dostaną między MEDIUM a MEDIUM-LOW ..to może tez warto przestać odpowiadać tak kierownictwu w kwestii ryzyka i strat? :)