Ten wpis będzie kontynuacją moich spostrzeżeń i wątpliwości dotyczących tzw. “jakościowych” metod analiz ryzyka. Poprzednie wpisy (chronologicznie):
Wprowadzenie
Powtórzmy sobie czym jest dla nas ryzyko? Jest ono naszą niepewnością co do wystąpienia niepożądanych zdarzeń. Chcemy tę niepewność zredukować do jakichś mierzalnych wartości, za pomocą estymacji, biorąc za podstawę dostępne nam dane. Na przykład: Twierdzę, że w mojej firmie, z pewnością na poziomie 90% czas rozwiązania incydentu bezpieczeństwa zawiera się w przedziale od 1h do 48h A następnie, logicznie przedstawić numeryczny obraz (rozkład) ryzyka w funkcji tej zredukowanej niepewności. Przydadzą nam się też równania Bayesa, jako że nieprzyjemne zdarzenia w obszarze cyberbezpieczeństwa rzadko występują niezależnie od siebie.
Czas, by zaproponować alternatywę dla nielogicznej, pseudo-matematycznej i w gruncie rzeczy, dającej fałszywy obraz i fałszywe poczucie pewności ryzyka, metody jakościowej z heat mapami.
Wykorzystana literatura i opracowania
W poprzednim wpisie dotyczącym tego obszaru dość niezgrabnie przedstawiłem tzw. “subiektywistów” nazywając ich Bayesowcami. Wątpliwości wobec macierzy ryzk i zainteresowanie metodą ilościową zaproponowaną przez pp. Hubbarda i Seiersena w ich “zielonej książce” doprowadziły do mnie do prób zgłębienia problematyki estymacji i procesów podejmowania decyzji, jak również do zagłębienia się w (równie fascynujący) obszar logiki bayesowskiej. Chcę lepiej zrozumieć logikę tego podejścia do ryzyka, aniżeli samą tylko mechanikę, czy algorytm postępowania i stosowania poszczególnych technik.
Tak natrafiłem na świetnie napisaną (przez matematyka dla prawie-nie-matematyków) książkę “Bernoulli’s Fallacy” doktora matematyki z Berkeley - Aubreya Claytona. Przy czym, wszyscy trzej autorzy w bibliografii swych prac wymieniają i cytują innego zwolennika stosowania wnioskowania bayesowskiego dla opisu zjawisk i stosowania w nauce - nieżyjącego już uczonego - fizyka kwantowego - Edwina T. Jaynesa. Jego “Teoria prawdopodobieństwa” jest pełną pasji polemiką z wnioskowaniem statystycznym jako jedyną właściwą metodą szacowania prawdopodobieństwa stawianych hipotez. A także postulatem rozszerzenia logiki stosowanej w nauce o wnioskowanie bayesowskie. Pan Clayton opublikował bardzo przystępnie poprowadzony cykl wykładów na temat teorii prawdopodobieństwa wg E.T. Jaynesa. Aktualnie, jestem gdzieś w połowie tych wykładów i nabieram odwagi do zmierzenia się z “Teorią..” E.T. Jaynesa.
Tu, mały wtręt, być może autorzy ISO-31010:2019 (“Risk Assessment Techniques”) też czytali podobne lektury, ponieważ po aktualizacji, norma ta, już nie promuje heat map a właśnie wnioskowanie bayesowskie (między innymi).
Szkoła subiektywistyczna
Dlaczego “subiektywistyczna”? Bo wykorzystująca logikę równań Bayesa i związane z tym wnioskowanie do zabawy z szacowaniem prawdopodobieństwa. Zresztą, w tym podejściu argumentuje się (Bruno de Finetti w wydanej w 1975 roku “Theory of Probability”) iż nie ma czegoś takiego jak obiektywnie zmierzone prawdopodobieństwo (ang. objective probability) Każdy jego pomiar czy estymacja zawsze będą subiektywne, ponieważ bazuje ono na subiektywnym pojmowaniu rzeczywistości i dostępnych danych. Ponad to, we wnioskowaniu bayesowskim, istotną rolę pełni subiektywna wiedza jaką posiada stawiający hipotezę, która warunkuje prawdopodobieństwo a priori. A więc daje szanse na wykorzystanie ogromu wiedzy i danych ekspertów od cyberbezpieczeństwa, ale wiedza jaką tacy eksperci dysponują, dane historycz{ne i ich zrozumienie będzie się różniło wobec innych danych i innych ekspertów z innej firmy. Ich zdolności estymacji, poziom kalibracji i rózne ludzkie ograniczenia też będa miały na to wpływ. Poniższy zapis jest notacją prawdopodobieństwa jakiejś hipotezy (np. Czy nasz internetowy portal ulegnie hackerom w ciągu kolejnych 12 miesięcy?):
P(H|DX)
czyli, jak prawdopodobna jest hipoteza (H), jeśli mamy dane (D) i wiedzę wcześniejszą (X). I to jest niejako naturalny kandydat do zastosowania w metodach ilościowych szacowania ryzyka, stosując ją wraz metodami estymacji ilościowej już istniejącej wiedzy. Dlaczego? Ano dlatego (co podkreślają autorzy “zielonej książki”), że w cyberbezpieczeństwie mamy historię różnych zdarzeń, chociażby w “naszej” firmie, czy w firmach o podobnym profilu lokalnie, w kraju czy na świecie. Dysponujemy też ogromną masę danych czekających by je wykorzystać. Nie musimy przeprowadzać szeroko zakrojonych eksperymentów populacyjnych aby oszacować ryzyko straty ze względu na problemy w obszarze cyberbezpieczeństwa.
Wielebny Bayes wkracza do gry
Dla wielebnego Bayesa, żadna hipoteza nie jest ani kategorycznie odrzucona, ani jednoznacznie (tj. 100-procentowo) pewna. Dla wnioskowania bayesowskiego, ważne jest to co obserwujemy i rozumiemy. A potem logicznie stosujemy w formułowaniu naszych hipotez. Co też implikuje sytuacje, gdzie dla naszej firmy P jakiegoś niepokojącego zdarzenia może mieć np. 35% a dla innej firmy 48% i to z różnych powodów. Wymieniony wcześniej zapis prawdopodobieństwa w przyjętej przez Claytona, de Finettiego i Jaynesa (a trafiającej do mnie) notacji:
P(H|DX) jest prawdopodobieństwem a posteriori. A całe równanie (ang. product rule) wygląda tak:
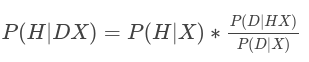
gdzie:
P(H|X) - nasze prawdopodobieństwem a priori, warunkowane wiedzą X,
P(D|HX) - nasze prawdopodobieństwem wiarygodności sampla danych (próbkowania), dla naszej hipotezy i wiedzy,
P(D|X) - jak prawdopodobne są nasze dane wg dostępnej i zrozumiałej przez nas wiedzy
Przy czym, warto tutaj podkreślić, jeszcze jeden krytyczny warunek stosowania logiki bayesowskiej. Zawsze musimy odnosić szacowanie naszej hipotezy do conajmniej jednej kontr-hipotezy. Posługując się tutaj twierdzeniem, że suma prawdopodobieństwa hipotezy (że “coś”) i prawdopodobieństwa negacji tej hipotezy (że “nie-coś”) równa się 1.
P(H|X) + P(~H|X) = 1
W ten sposób wyliczone przez nas P danej hipotezy a posteriori w odniesieniu do P a posteriori negacji tej hipotezy, da nam odpowiedź - jakie mamy szanse na wystąpienie jakiegoś zdarzenia w proporcji do szans jego nie wystąpienia. A więc odzwierciedla naturalne dla nas zrozumienie prawdopodobieństwa, którym posługujemy się chyba nawet codziennie - mówiąc, że “no, na 70% będzie dziś padać”..
Nieodległy przykład
Za górami, za lasami, żył sobie dziad z babą. Któregoś dnia baba poszła do pracy, a dzień zakończyła imprezą, gdzie też świetnie się bawiła. Impreza była zorganizowana w stosunkowo niewielkim pomieszczeniu dla 20+ osób, ale było fajnie. Nadszedł weekend i baba, przy niedzieli, poczuła się źle. Katar, kaszel, ból głowy, no ogólnie dość covido-podobnie. Dziad poszedł do apteki kupić babie test, który baba niedługo potem wykonała. Najpierw jednak, dziad testowi się przyjrzał, zezując na drobne literki w ulotce testu.
Dostępne dane (X)
Test antygenowy to “BOSOM Biotech antigen test”. Dziad wyczytał, że Kanadyjczycy podają jego skutecznosc na 97.48% jeśli jest wykonany na poczatku choroby, kiedy symptomy wlasnie wystepuja. No i tu test babie pozytywny wyszedł. Druga istotna informacja - baba była szczepiona trzy razy. Przy czym skuteczność szczepionki wobec Omikrona (następca Delty) spada do ok. 45% po 10 tygodniach. A baba szczepiła się dość dawno. Zatem tę skuteczność ciachniemy babie jeszcze o połowę na, powiedzmy 25%. (Dziad nigdzie nie doczytał, czy ten spadek jest liniowy czy jakiś inny).
P(H|X)
Biorac jako a priori szanse że miała ok. 80% przebywając dłużej niż 1h w małym pomieszczeniu z 20-ma osobami, przy założeniu ze ktoś tam zarażał. Jakąś tam ochronę zapewniały jeszcze wspomnienia po szczepionce. Przyjmując powyższą skuteczność tych wspomnień na poziomie 25%, dziad otrzymał P a priori równe 60%. Zatem hipoteza odwrotna przyjmie wartość 40%.
P(D|HX)
Dziad na ulotce testu wyczytał, że sprawność testu jest 97,48%. Drapiąc się po prawie łysym łbie przyjął przedział ufności 95% i pomnożył jedną wartość przez drugą - wyszło 0,916. Dla hipotezy odwrotnej prawdopodobieństwo próbkowania przyjmie wartość podaną “false positives” - czyli, przetestowani pozytywnie wciąż mają szansę pół-na-pół, że test ich okłamał (w przepisowych warunkach testowania).
No to teraz posługując się wyżej wymienionymi równaniami Bayesa, można oszacować prawdopodobieństwo, że baba miała covida [2]:
| Hipoteza: | P(H|X) | Próbka P(D|HX) | P(H|X)P(D|HX) | Proporcje P(H|DX) |
| ma Covid | 0,6 | 0,916 | 0,55 | 63,7% |
| nie ma Covida | 0,4 | 0,5 | 0,2 | 36,3% |
Prawda, że lepiej to brzmi, kiedy dziad babie oznajmił, że w 6-ciu przypadkach na 10, ma szansę, że jednak tego covida ma. Zamiast pleść, że ma “prawie na pewno” tego covida? Babie, co prawda, było wszystko jedno, bo się paskudnie czuła. Dziad jednak był z siebie dumny.
Przykład z tzw. branży
Przychodzi pan prezes do swojego naczelnego eksperta d/s ryzyka cyberbezpieczeństwa i pyta o to jak mamy zabezpieczone nasze systemy przed wyciekiem danych. Czytał w prasie, że ostatnio straszne kary nakładają na te firmy, którym dane “wyciekły” w ten czy inny sposób. Pan ekspert, bedąc biegłym w swej specjalności, szybko przedstawia Panu prezesowi wyniki krótkiej analizy.
Hipoteza i dostępne dane (X)
Jakie jest P wycieku danych w aplikacji internetowej, wiedząc że: w aplikacji internetowej istnieje podatność exploitowalna zdalnie, i to że takie włamanie związane z ta podatnością już miało miejsce u konkurencji, która w ten sposób straciła dane. Skanery podatności, ustawicznie testowane i doskonalone wykazują 15% false negatives i 5% false positives.
Założenie, wiemy że średnio tego typu incydenty z wykorzystaniem tej podatności, w naszej działce biznesowej przy tej wielkości przedsiębiorstw mają P=20% (np. 20 firmach na 100 w ciągu roku), inne niż dla tej podatności, wektory ataków mają skuteczność 0.01 (1%) i wystąpiły w jednej podobnej firmie na 100, przez ostatnie 12 miesięcy.
Oprócz tego, nasz ekspert formułuje 3 kolejne hipotezy:
- hipoteza przeciwna: P(~H|DX) tj. brak wycieku danych przy wykrytej podatności,
- hipoteza wycieku danych przy braku tej konkretnej podatności: P(H|~DX),
- hipoteza przeciwna do powyższej: P(~H|~DX)
P(H|X) - P wycieku danych pod warunkiem istnienia takiej podatności, P(H|X’) - P wycieku danych jeśli tej akurat podatności nie ma (ale są inne) - 0.01 P(D|H,X) - P że istniała podatność w naszym systemie, ponieważ nastąpił wyciek danych z wykorzystaniem tejże podatności
| Hipoteza: | P(H|X) | Próbka P(D|HX) | P(H|X)P(D|HX) | Proporcje P(H|DX) |
|---|---|---|---|---|
| Wyciek danych, stwierdzona podatność | 0,2 | 0,95 | 0,19 | 28% |
| Brak wycieku w nast. tej podatności | 0,8 | 0,85 | 0,68 | 72% |
| Wyciek danych przy braku podatności | 0,01 | 1 | 0,01 | 1.18% |
| Brak wycieku i brak tej podatności | 0,99 | 0,85 | 0,8415 | 98.82% |
Odpowiedź brzmi: Panie prezesie, melduję wykonanie zadania, pokazuję i objaśniam:
Jeżeli nasz doskonały skaner podatności wykryje dziurę przez którą wyciekły już dane naszej konkurencji, to mamy 28% szans, że spotka nas to samo. A jeżeli nie wykryje tej podatności, to biorąc pod uwagę inherentną niedoskonałość skanerów, które mimo naszych usilnych i profesjonalnie przeprowadzonych starań, wciąż mają niezerową szansę podać fałszywe wyniki, wciąż jest 10% że padniemy ofiarą ataku, który może doprowadzić do wycieku danych. Nie mniej jednak, mamy od 72 do 99% szans, że pozostaniemy bezpieczni przez kolejne 12 miesięcy, jeśli chodzi o grupę ataków wykorzystujących podatności w aplikacji webowej wystawionej do internetu.
Podsumowanie tej części
W ostatnim przykładzie, gdybyśmy chcieli się pokusić o estymację wpływu zabezpieczeń, musielibyśmy zastosować dodatkowe twierdzenia logiki bayesowskiej. O tym będzie w kolejnym wpisie. Ten bieżący miał na celu pokazanie, jak w dość prosty sposób można zastąpić nie-logikę, logiką.
Najważniejsze to nabycie umiejętności redukowania niepewności i estymacji na podstawie dostępnych danych (Clear, Observable, Useful) i wiedzy eksperckiej. Prócz tego, stosowanie kryteriów właściwej dekompozycji złożonych hipotez, tak aby: sformułowana hipoteza ułatwia estymację i nie wprowadzała jeszcze więcej elementów o charakterze spekulatywnym (zaciemniając obraz). Tego typu wyliczenia często się też weryfikuje (a nie jak w przypadku macierzy ryzyk - maluje raz do roku - jest to kolejny nonsens). Przy czym za podstawę a priori do kolejnych wyliczeń bierzemy poprzedni wynik a posteriori lub jeśli mamy lepsze dane (albo lepsze ich zrozumienie) stosujemy je do wyliczenia nowego a priori.
Na pewno przydadzą się podstawy wiedzy z zakresu logiki bayesowskiej (znajomość dwóch podstawowych równań).