W poprzednim odcinku, opisałem czym jest macierz ryzyka i podstawowy problem z pomieszaniem pojęć. Ta istotna bariera w zrozumieniu czym ryzyko jest a czym nie jest, nie jest jedyną przeszkodą. Poniżej przedstawię kolejne istotne problemy, które są przynależne tej metodzie przedstawiania ryzyk.Są to częściowo moje własne spostrzeżenia jak również wnioski z pogłębionej analizy problemu w oparciu o dostępną literaturę. Będzie trochę srogo.. :)
Metody eksperckie
Problemy z metodami eksperckimi opisałem w poprzednim wpisie. Prócz tamże opisanych, cierpimy na jeszcze inne dolegliwości poznawcze, takie jak awersja do niepewności, przekonanie o nieomylności i stronniczości. Te w połączeniu ze zwyczajnym brakiem wiedzy, brakiem treningu (szybkie myślenie vs wolne myślenie) i wyżej opisanym bałaganem pojęciowym - prowadzą do tego, że metody te są często zbliżone do wróżenia z fusów. A wszyscy wokół udają zrozumienie. Przykładem może być technika samooceny (ang. risk self-assessments), dość popularna - mogłaby być przydatna, ale jest do niczego.
Pomylenie statystyki z prawdopodobieństwem
Jakiś czas temu buszując tu i tam po internecie natrafiłem na ślad strasznie poważnego konfliktu “frequentists vs bayesians”. Nawet nie bardzo wiem jak to poprawnie przetłumaczyć - może frekwencjonistów z bayesowcami? Ogólnie rzecz ujmując, chodzi o pewną pułapkę myślową, w którą dość powszechnie wpadamy, kiedy wydaje nam się, że P jakiegoś zdarzenia zależy wyłącznie od liczby wystąpień w jakiejś próbie. I od razu przyjmujemy załóżenie, że takie zdarzenie czy zjawisko występuje w szeroko pojętej przyrodzie z taką właśnie częstotliwością.
Podczas gdy bayesowcy, mówią - hola, hola.. drodzy Państwo, jeśli mamy liczbę wystąpień w próbie to możemy uznać to za prawdopodobieństwo a priori - wstępne, które należy zweryfikować posługując się równaniami ministra Bayesa.
Przykładowo, w naszym obszarze byłoby to coś w rodzaju:
Frekwencjonista mówi: “W ciągu roku wystąpił incydent (H) z wykorzystaniem podatności (X) w 20 firmach na 100. Tak średnio. A zatem P takiego zdarzenia to 20%. Wobec tego, plasujemy nasze zdarzenie, zgodnie z tabelką, jako ŚREDNIE! Taadaaam.”
A bayesowiec, zrobi facepalm i powie tak: “Przyjmijmy założenie: wiemy że średnio tego typu incydenty z wykorzystaniem tej podatności, w naszej działce biznesowej przy tej wielkości przedsiębiorstw mają P=20% (w tych 20 firmach na 100 w ciągu roku), inne niż dla tej podatności, wektory ataków mają skuteczność 0.01 (1%) - czyli w przypadku innych podatności ofiarą pada 1 na 100” Wobec tego, mruczy dalej pod nosem - “Spróbujmy ustalić jakie jest P wycieku danych w aplikacji internetowej, wiedząc że: istnieje podatność exploitowalna, i to że takie włamanie zwiazane z ta podatnością już miało miejsce u konkurencji, która takie dane straciła. Skanery podatności wykazują 5% false negatives”.
A co więcej, jeśli nasz bayesowiec, policzy kontr-hipotezę, jakie jest P że przy w/w warunkach zdarzenie nie wystąpi, to przez prostą proporcję dostaniemy wiarygodną liczbę, jaką właściwie mamy szansę na wtopę.
I Bayesowcy chyba troszkę nawet wygrywają, kiedy ISO 31010 wydanie z 2019 roku, wyraźnie wskazuje, że analizę bayesowską stosujemy przy szacowaniu prawdopodobieństwa właśnie. W poprzednim wydaniu tej normy z 2010 roku, takiego wskazania nie było.
Niespójność
Każda metodyka wykorzystująca rachunek prawdopodobieństwa, powinna być zgodna z podstawowymi właściwościami tego rachunku. Jest to dość powszechny postulat, sformułowany przez.. hmm, kogoś mądrego w 1999 roku (tyle pamiętam, a nie zarejestrowalem żródła) - Zapewnia to spójność takiej metodyce i to, że jest po prostu uzyteczna.
-
Istotność: X > 0 to p(X) > 0; Kiedy zdarzenie ma jakieś policzalne ryzyko, to metryka tego ryzyka również powinna mieć jakąś niezerową wartość (nie może być zerowa). I nawet dla skali porządkowej, ten warunek zachodzi.
-
Monotoniczność: Jeśli X ≥ Y to p(X) ≥ p(Y); Jeśli dane zdarzenie ma wyższą metrykę ryzyka niż kolejne, to te kolejne powinno mieć metrykę co najmniej równą temu pierwszemu, bądź wyższą. I tutaj już mamy problem, przez tę skalę porządkową. Zdarzenie z wyższą metryką ryzyka, może być niżej na skali porządkowej, niż inne zdarzenie z niższą metryką.
-
Inwariancja skalowa: p(X + α) = p(X) − α ; Oznacza to, że przy redukcji ryzyka jego metryka maleje proporcjonalnie. No i znowu, skala porządkowa nie zapewnia, że ta własność jest zachowana. Co więcej, ta własność powinna zapewniać, że jeśli redukcja o jakąś wartość zaszła dla kilku zdarzeń o określonej relacji (proporcji porządkowej w tym wypadku), to ta relacja po redukcji jest zachowana.
-
Subaddytywność: p(X + Y) ≤ p(X) + p(Y); Tzn. że całkowitego prawdopodobieństwa nie oblicza się przez zwykłe zsumowanie prawdopodobieństw. I nie jest to jasne dla matrycy ryzyka, która niejako a priori zakłada, rozpatrywanie zdarzeń, występujących niezależnie (co w cyberbezpieczeństwie często nie jest prawdą, albowiem zawsze zachodzi jakiś łańcuch(y) zdarzeń albo wspólnie albo następczo)
-
Dodatnia homogeniczność: dla α > 0: p(αX) = αp(X) ; Zapewnia że metryka ryzyka jest blisko związana z samym ryzykiem. Jeśli ryzyko się podwaja, to jego metryka również. No i tutaj również mamy problem, bo R o P z początkowej wartości dobranego przedziału o metryce 2, nawet jeśli podwoimy jego wartość nadal może pozostać z wartością 2.
Zdarzenia zależne czy niezależne
Jak już nadmieniłem nieco powyżej, matryca ryzyk rozpatruje poszczególne zdarzenia jako niezależne. Nnawet jeśli są poprawnie opisane a ich hipotezy dobrze sformułowane. Analityk po prostu bierze liste scenariuszy i w myśl przyjętej metodyki, szacuje P i straty i z tabelki wychodzą mu miary dla wszystkich zdarzeń.
W ten sposób powstaje taka ładna tabelka (bardzo poważnie i nieco magicznie wyglądająca):
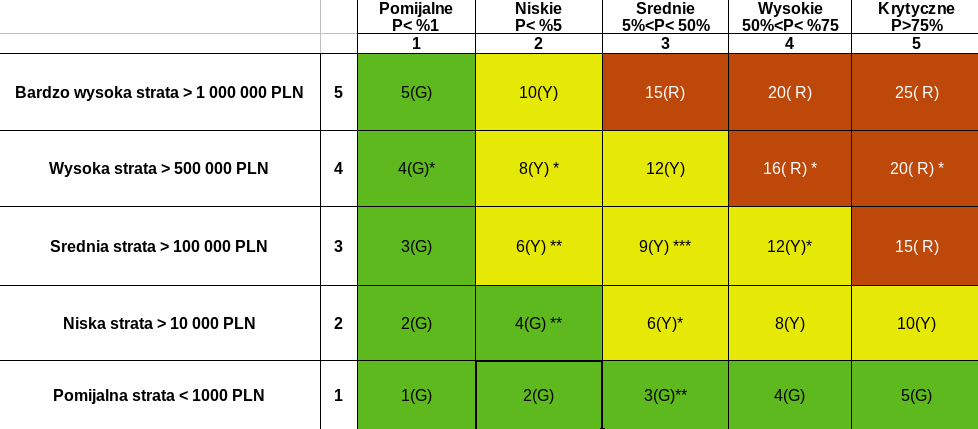
I teraz w przykładowym raporcie z badania audytowego stoi pieknie napisane, że WYKRYTO: tylez ryzyk WYSOKICH, tyleż ŚREDNICH i tyleż NISKICH. Zgodnie z przyjęta metodyką..tu następuje precyzyjny opis co zostało znalezione, do czego może prowadzić (żadnej inwencji, wzięte z tabelek pomocniczych na podstawie “standardów). I teraz jak ongi w czekoladkach adwentowych z Niemiec, każde otwarcie okienka to czekoladka. Przy czym kolejność otwierania okienek zależy od priorytetów wprost wynikających z metryk.
No troszkę bez sensu.
Istotne pytania na które trudno znaleźć odpowiedzi czytając taki raport, to:
- A co jeśli na raz wystąpiłyby: 3 zdarzenia NISKIE i 2 ŚREDNIE? Czy to implikuje jakąś odrębną akcję zaradczą?
- Jeżeli stosowano tylko podejście frekwencjonistyczne - to mamy sprzeczność logiczną. Bo kiedyś nie wystąpiło takie zdarzenie z prostego powodu - nie mieliśmy takiej aplikacji lub technologii na pokładzie.
- A jeśli tych średnich i lekko-pół-średnich jest tyle, że w sumie ich strata przekracza wielkość tego jednego WYSOKIEGO a ich P mieści się w przedziale od 5 do 75%, czyli de facto niepewność ich estymacji jest dość wysoka - to tylko obserwujemy?
- A jeśli te średnie, się wydarzą (cholera wie kiedy, ale szansę mają przecież sporą) i w konsekwencji stworzą świetne warunki do wystąpienia jeszcze poważniejszego zdarzenia? To gdzie tego szukać w tej tabelce?
- A co jeśli są to jednak zdarzenia zależne - często tak bywa (patrz matryca MITRE ATTACK), że szansa powodzenia ataku wzrasta jeśli poprzednie zdarzenia się wydarzyły. Poza tym, badanie zazwyczaj dotyczy jakiegoś wybranego obszaru IT albo aplikacji, bądź jej eko-systemu. Wobec tego rozpatrywanie zdarzeń bezpieczeństwa jako niezależnych od siebie w takim obszarze da nieprawdziwy obraz.
ciąg dalszy nastąpi..
Bibliografia
- J. Freund, J. Jones “Measuring and managing information risk”
- D.W. Hubbard, R. Seiersen “How to measure anything in Cybersecurity Risk”
- Philip Thomas, Reidar B. Bratvold, J. Eric Bickel “The Risk of Using Risk Matrices”
- Michael Krisper “Problems with Risk Matrices Using Ordinal Scales”
- “Risk Management - Risk assessments techniques (IEC:31010-2019) BSI Standards Publication”
- Aubrey Clayton “Bernoulli’s Fallacy”