Są takie książki do których trzeba się mentalnie i merytorycznie przygotować. A kiedy już się po nie sięgnie ich zawartość jest starannie czytana, ..i czytana ..i czytana, treść “obracana” w głowie, aż do pełnego zrozumienia. Ale też nie, że “Achaaa.. to tak działa!” i siup, następny rozdział. Trzeba to przerobić praktycznie.

Jeśli rozdział zawiera rozwiązanie jakiegoś problemu w sposób programistyczny, to wypada również podejść do takiego problemu samodzielnie i znaleźć rozwiązanie w ten czy inny sposób. Więc czasem robi się z tego wielomiesięczne studium. Tak było w przypadku “How to measure anything in cybersecurity”, tak jest też w przypadku “The Metrics Manifesto”. Tę drugą właśnie studiuję, wciąż wracając do tej pierwszej.
“We confuse what’s easy to measure, like bullet holes in returned planes, with what is important to measure, like bullet holes in downed planes. We deceive ourselves by measuring only what is obvious, forgetting the goal of our measurement” [R. Seiersen, “The Metrics Manifesto”]
Metryki bezpieczeństwa powinny odpowiadać na całkiem zasadnicze pytania, które zadaje sobie (chyba prawie) każdy odpowiedzialny kierownik czy ekspert dziedzinowy, a także stanowić dane wejściowe do szacowania ryzyka w danym obszarze cyberbezpieczeństwa.
Zamiast liczyć ileż to podatności zostało załatanych miesiąc do miesiąca, czy rok do roku - bo to są tylko metryki logistyczne na zasadzie - tyle a tyle cementu dowieziono - można zadać sobie pytanie: ile średnio, każdego dnia w roku mam niepołatanych podatności o istotności krytycznej w obszarze kluczowych aplikacji. Albo zamiast liczb ile rozwiązano incydentów, jaki jest trend współczynnika incydentów rozwiązanych do nierozwiązanych w podziale na aplikacje czy obszary (np. on-prem vs cloud). Czy też, na podstawie danych z przeprowadzonych testów, oszacować ryzyko phishingu - czyli jaką procentową szanse możemy założyć, że na 1000 wysłanych emaili ileś osób jednak kliknie i obserwować ten trend miesiąc do miesiąca. To można robić i to w całkiem zautomatyzowany sposób. Wystarczą dane, python (albo R) i trochę umiejętności grzebania w danych.
Okazuje się, że naprawdę nie trzeba petabajtów danych, aby przygotować ciekawe metryki. Wystarczy prosty raport z wykrytych i usuniętych podatności w jakimś okresie.
Instalacja Jupytera
Dopóki nie spróbowałem, nie miałem pojęcia jakie to przydatne narzędzie w analityce danych. Środowisko Pythona mam już skonfigurowane z pipenv (łączy w sobie wygodę pip i venv). W danym katalogu projektowym odpalamy pipenv shell i wykonujemy:
$ pipenv install jupyter jupyterlab ipykernel
$ pipenv install numpy scipy pandas seaborn statsmodel scikit
$ python -m ipykernel install --user --name=metrics
$ pipenv run jupyter lab
W nowej zakładce przeglądarki uruchomi się UI Jupyter lab, gdzie należy wybrać kernel - metrics z uprzednio zainstalowanymi bibliotekami. Jeśli jednak jakiejś zabraknie to w linii kodu wystarczy wykonać !pipenv install <brakująca_biblioteka>.
Nieco teorii - tabele przeżycia
Zwane również tabelami trwania życia. Naturalnym skojarzeniem jest od razu ZUS. Nam chodzi o coś innego. Zbadanie rozkładu okresów jakie upływają między danymi zdarzeniami. Na przykład, między pojawieniem się podatności a jej usunięciem. Więc zdarzeniem terminalnym jest tu usunięcie podatności. Celem tabeli jest pomiar szans na przeżycie podatności w danym okresie albo inaczej - wyliczenie prawdopodobieństwa wystąpienia zdarzenia usunięcia podatności w danym okresie. W tym kontekście upraszczając: podatność jest procesem, który wystąpił (data wykrycia) i który mógł zostać przerwany (terminacja, śmierć) przez usunięcie (załatanie podatności, podbicie wersji biblioteki itd.).
Kiedy już wyznaczymy sobie interwał czasowy, w którym chcemy złapać wszystkie zdarzenia wystąpienia podatności i jej usunięcia, musimy wykonać jeszcze dwie czynności - odfiltrować zdarzenia które:
- zaczęły się ale nie skończyły w przyjętym interwale czasowym - ocenzurowane,
- zaczęły się w dniu prawej granicy interwału albo po tym dniu - odrzucone.
Przykład poniżej, przypuśćmy że badamy sobie raport z pierwszej połowy roku, gdzie mamy 8 podatności. V1, V2 i V7 cenzurujemy a V8 odrzucamy.
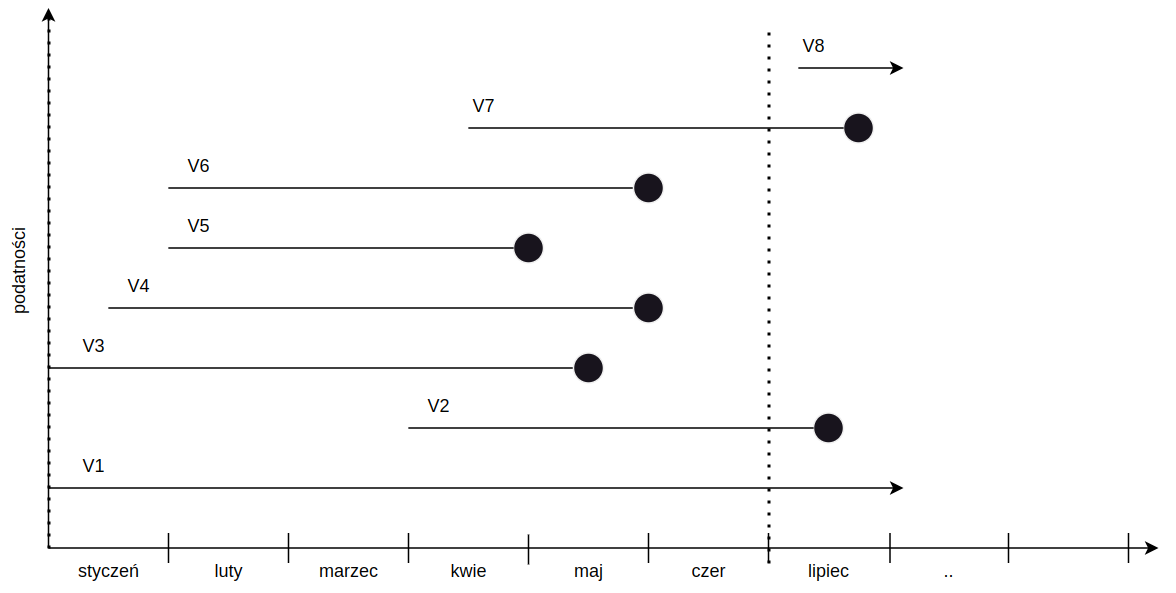
Python i estymator
Ładujemy plik CSV z raportem podatności do DataFrame:
1
2
3
!wget https://raw.githubusercontent.com/ribsy/mdata/main/tmm_start.csv
Nagłówki w pliku CSV stają się nazwami kolumn w DataFrame, w naszym przypadku musimy lekko skorygować te nazwy zamieniając kropki na znak podkreślenia.
1
2
3
4
5
import pandas as pd
df = pd.read_csv('tmm_start.csv')
df.rename(columns = {'first.seen':'first_seen', 'last.seen':'last_seen', }, inplace = True
Nasza tabela nie zawiera jeszcze dwóch kolumn istotnych dla naszej analizy. Jedna to okres występowania podatności (czyli last_seen - first_seen) i status podatności - Ok, czy ocenzurowana. Pierwsza linijka kodu wylicza nam deltę dla każdej wartości kolumn last_seen i first_seen, druga linijka zmienia nam tę deltę na liczbę dni i pakuje do nowej kolumny o nazwie delta. A trzecia linijka sprawdza czy daną podatność trzeba ocenzurować i w zależności od tego w kolumnie status pakując tam 0 lub 1. W ostatniej linii filtrujemy sobie dane i pakujemy je do nowej tabeli DataFrame.
1
2
3
4
5
6
7
8
9
from datetime import datetime as dt
from datetime import timedelta
delta = [(dt.strptime(stop,"%Y-%m-%d") - dt.strptime(start,"%Y-%m-%d"))+timedelta(days=1) for start, stop in zip(df['first_seen'],df['last_seen'])]
df['delta'] = [x.days for x in delta]
df['status'] = [1 if (dt.strptime(stop,"%Y-%m-%d") < dt.strptime('2020-12-31',"%Y-%m-%d")) else 0 for stop in df['last_seen']]
df_flt = df[(df.idTeam == 1) & (df.group == 1) & (pd.to_datetime(df.first_seen) <= pd.to_datetime('2020-10-01'))]
I to właściwie tyle. Dane mamy przygotowane. Teraz wykorzystamy je do (wyliczenia i przedstawienia graficznego) odpowiedzi na pytanie: jaka liczba podatności zostaje usunięta po X dniach z wyliczonym prawdopodobieństwem. Do tego celu użyty został estymator Kaplana Meiera. Estymator ten prognozuje funkcję przeżycia danej frakcji (podzbioru) podatności.
Na początku, zdefiniowałem dwa kryteria (dwie frakcje - podatności krytyczne i high), a potem już poszło sprawnie. Wywołanie objektu KaplanMeierFitter() i zastosowanie metody fit gdzie podałem wyliczoną deltę i status dla każdego wiersza naszej tabeli df_flt.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import datetime
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt
critical = ((df_flt.severity == 'extreme') | (df_flt.severity == 'critical'))
high = (df_flt.severity == 'high')
ax = plt.subplot()
kmf = KaplanMeierFitter()
kmf.fit(durations=df_flt[critical].delta, event_observed=df_flt[critical].status, label='Critical vulns')
kmf.plot_survival_function(ax=ax)
kmf.fit(durations=df_flt[high].delta, event_observed=df_flt[high].status, label='High vulns')
kmf.plot_survival_function(ax=ax)
plt.title('Vulns survivability based on their relevancy')
plt.show()
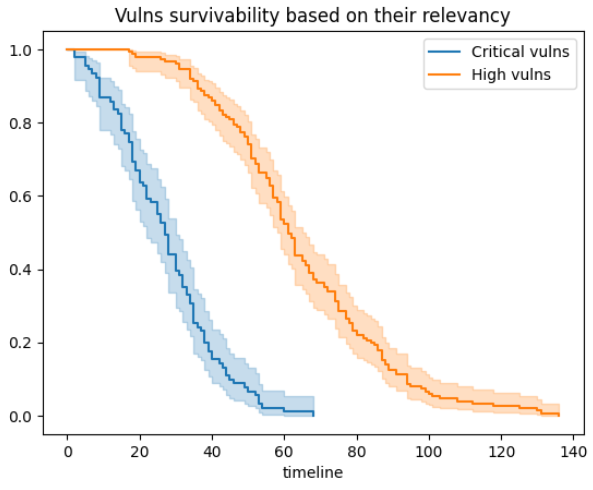
Jaką informację mamy zawartą na powyższym wykresie (oś x - liczba dni, oś y - % liczby zdarzeń)? A taką że - w zadanym okresie:
- Podatności krytyczne są szybciej usuwane niż te o statusie
High(to dobrze, ale nie zawsze jest oczywiste), - Srednio 50% usuwanych podatności krytycznych jest usuwana po ok. 23-29 dniach a
Highpo 58-62 dniach,
Mając różne atrybuty podatności w raporcie, w rodzaju: która aplikacja, który zespół, itd. możemy te podatności badać w rozbiciu na różne podzbiory (frakcje). Poniżej, przykład podobny do pierwszego, ale niosący dodatkową informację jak sobie różne zespoły radzą z usuwaniem podatności:
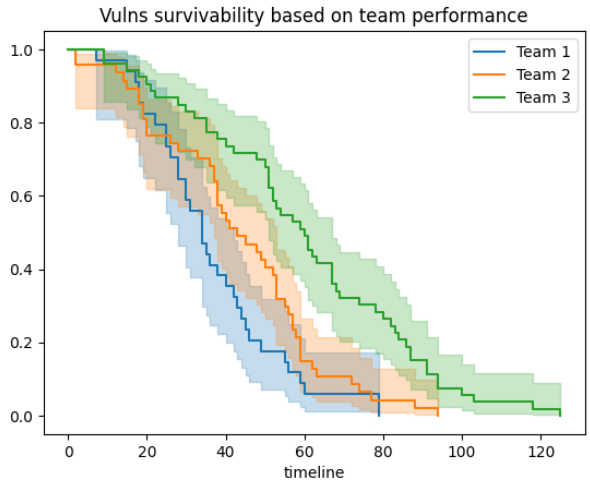
Warto zauważyć, że im więcej danych, tym przedziały wiarygodności, będa węższe a więc nasze prognozy - trafniejsze. I to tyle na razie. Poza tym można podobną analizę zastosować do zidentyfikowanych zagrożeń, obsługi incydentów bezpieczeństwa, z badaniem czy SLA są dotrzymane itd. Całość kodu w Jupyter notebook
Bibliografia: